Team Kyutech
Kyushu Institute of Technology Nakakuki lab
Address
Kyushu Institute of Technology 680-4 Kawazu, Iizuka, Fukuoka, Japan
2. Design
The function of the molecular governor arises from flux regulation through a permeable membrane. Therefore, the membrane is a key element in our system, and a membrane design with an appropriate transmission rate has to be established. In this section, we summarize how to design a membrane with a desired transmission rate. Finally, we show simulation results to validate the design method. As you know, it is not a trivial task to make an appropriate permeable membrane for nano-scale molecules. Rather, it is a challenging task, which is why we attempted it in BIOMOD2014.
2.1 Membrane as a key element in our device
Fig1. Image of membrane (red ball, a molecule; blue plane, a permeable membrane)
A technical highlight of our product is an integral controller for regulating the concentration of a specific DNA strand as an output signal to a desired level using a series of DNA strand displacement reactions in combination with a permeable membrane (Fig. 1). In what follows, we explain a design method for a permeable membrane that a DNA strand can pass through with a desired transmission rate.
Fig2. A flow of single-stranded and double-stranded DNAs through the membrane (orange, a single-stranded DNA; green, a double-stranded DNA; fresh-colored division, a permeable membrane with some pores)
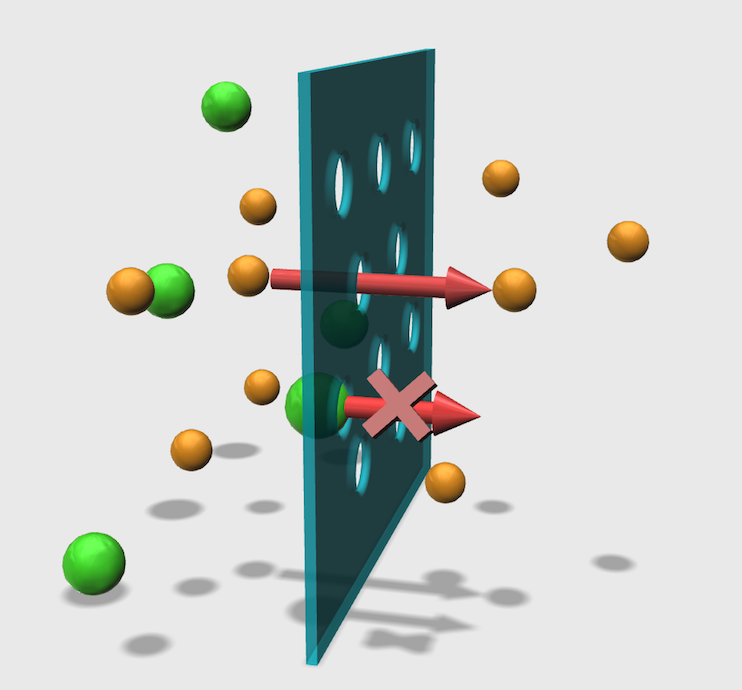
Fig. 2 illustrates the flow of a single-stranded DNA and double-stranded DNA molecule through a membrane. The single-stranded DNA can permeate the membrane because it is smaller than the pore, whereas the double-stranded DNA, which is bigger than the pore, cannot permeate the membrane. Although the ability of a molecule to pass through the membrane is simply decided by the size of the pore, we have to establish the design theory for realizing a desired transmission rate, which is a challenging task.
2.2 How to design membrane
The design objective is to determine the structural specifications of the permeable membrane (pore size [nm], membrane thickness [nm], and an open area ratio [-]) when a desired transmission rate [1/s] is given.
2.2.1 Size of DNA strand
Fig.3. Assumption on the size of DNA strand in our design theory (left, a DNA strand; right, its expediential shape in our theory)
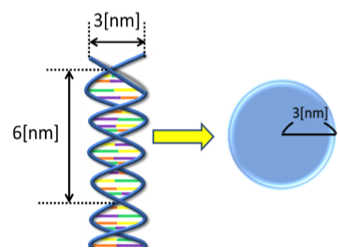
First, we consider the size of a DNA strand as a solute that permeates the membrane. For the sake of simplicity, we suppose that the shape of a DNA strand is ball-like (Fig. 3). The assumption would be valid if we estimate a larger size for the ball. For example, a 3-nm in diameter would be a reasonable choice for a short-stranded DNA. If another value is chosen for the diameter, that value is used in the following calculation.
2.2.2 Design theory for membrane with a desired transmission rate
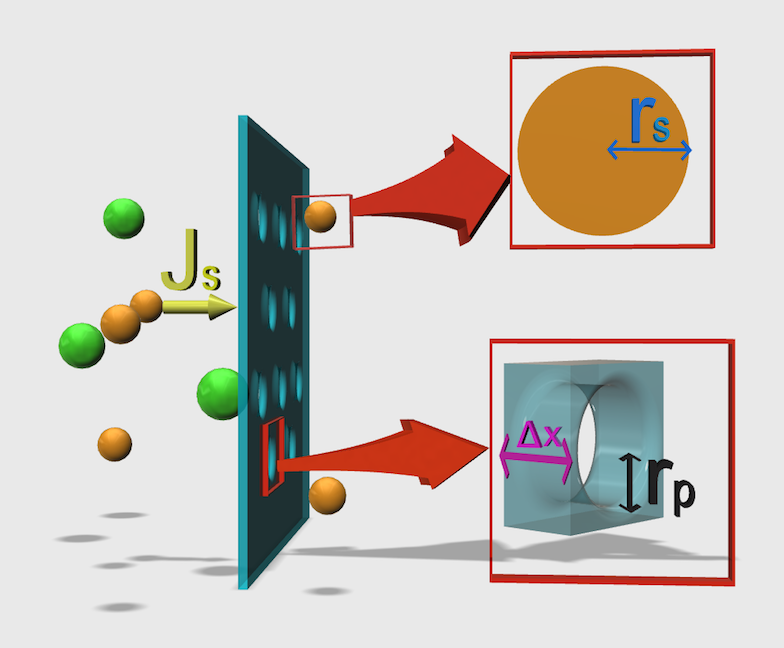
We employed a general model called “pore mode” to derive our design theory. In this model, the solute is considered to be a hard ball, and a pore is a route in the membrane cylinder (Fig. 4). All parameters are summarized in Table 1.
Fig4. Assumption and the parameters in the pore model.
To make a membrane with a desired transmission rate [1/s], we need the structural specifications such as the pore size [nm], membrane thickness [nm], and open area ratio [-]. However, the relationship between the macroscopic rate and the microscopic parameters is generally unclear. We propose a solution as follows:
Table1. Parametern in the pore model
Transmission phenomenon of permeate membranes is characterized by the following equations regarding flux
\begin{align}
\ R =
\frac{ {\rm C}_m-{\rm C}_p}{{\rm C}_m} =
\frac{\sigma[1-exp\bigl\{-\frac{-{\rm J}_v(1-\sigma)}{P}\bigl\}}{1-\sigma exp\bigl\{\frac{-{\rm J}_v(1-\sigma)} {P}\bigl\}}
\tag{1}
\end{align}
\begin{align}
\ {\rm J}_v =
\ {\rm L}_p(\Delta p-\sigma\Delta\Pi)
\tag{2}
\end{align}
\begin{align}
\ {\rm J}_s =
\ P({\rm C}_m-{\rm C}_p)+(1-\sigma)\overline{c} {\rm J}_v
\tag{3}
\end{align}
The relationship between the volume flux density and the structural parameters is given by the following three parameters:
\begin{align}
\ {\rm L}_p =
\biggl(\frac{rp^2}{8\mu}\biggl)\biggl(\frac{{\rm A}_k}{\Delta x}\biggl)
\tag{4}
\end{align}
\begin{align}
\ \sigma =
\ 1-{\rm S}_F(1+\frac{16}{9}q^2)
\tag{5}
\end{align}
\begin{align}
\ P =
\ D{\rm S}_D\biggl(\frac{Ak}{\Delta x}\biggl)
\tag{6}
\end{align}
where the radius of solution is given by
\begin{align}
\ {\rm r}_s =
\frac{KT}{6\Pi\mu D}
\tag{7}
\end{align}
Because no outside pressure is added to the system, we can ignore the volume flux of the solvent (Jv = 0); that is, the membrane permeation is due to the concentration difference between the cross-border rooms. Because the volume flux Jv is described by a transmission rate and the thickness of membrane, we obtain the following master equation for the design.
\begin{align}
\ k\cdot\Delta x =
\frac{KT}{6\Pi\mu {\rm r}_s}\cdot\biggl(1-\frac{{\rm r}_p}{{\rm r}_s}\biggl)^2\cdot\biggl(\frac{{\rm A}_k}{\Delta x}\biggl)
\tag{8}
\end{align}
See Fig. 5 for the detailed calculation. Although (8) is an indeterminate equation with three unknown parameters, we can computationally solve it. This is quite beneficial for a designer since we can choose a convenient combination of parameters to facilitate manufacturing!
Fig5. Detailed calculations for the master equation (8)
2.3 Validation with in-silico experiment
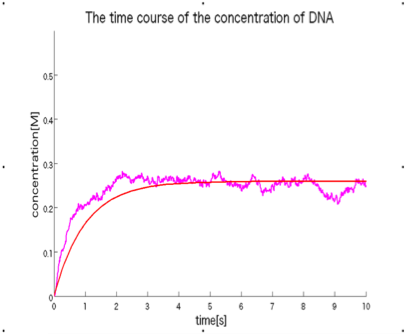
in this section, we will show a validation result for our method by using in-silico experiment. If a time-course data on a concentration change in the system, which is calculated with only a transmission rate k [1/s] based on chemical kinetics (ordinary differential equation-based simulation), coincide with that with only three structural parameters, a size of pore [nm], thickness of the membrane [nm], and a open area ration [-], based on particle simulation (stochastic simulation).
Fig.6 indicates a result on a stochastic particle simulation in which thepermeation phenomenon successfully occurs in-silico . Three structural parameters and transmission coefficient are in the Table. 2. Fig. 7 shows two kinds of time-course curves from the macroscopic ordinary differential equation-based simulation with only a transmission coefficient k and the microscopic stochastic particle simulation with only three structural parameters, indication that they have a similar time-course shape. Therefore, we conclude that our design method is theoretically correct of which validity is supported by in-silico experiments.
Table.2 Three structural parameters and transmission coefficient.
Fig.6 Stochastic particle simulation results. (red, molecule;bule, membrane)
