


1. Molecular Governor
1.1 Mission
Many diseases such as cancer and diabetes (visible health problems) are deeply tied to dysfunctions in intracellular systems (invisible nanoscopic phenomena). The intracellular system is rigorously controlled by biochemical reactions. If a dysfunction occurs in the system, it occasionally results in a serious situation and is considered to be unstable. A fundamental therapeutic method will be required to control intracellular systems that depend on concentrations of biochemical molecules. To this end, we propose the following remedies:
(1) A control theory for regulating the concentration of a target molecule using feedback control mechanisms.
(2) A method for creating a permeable membrane with a desired transmission rate on an impermeable membrane.
By applying (1) and (2), we will be able to control intracellular systems, and consequently transform unstable cancer cells into normal cells. However, in order to drive a cell system, we first have to establish a technique to access the intracellular system. Remedy (2) is a possible solution based on a simple idea. An existing application is shown in our movie. Please check it out.
1.2 What is Molecular Governor?
Almost all products, powertrains, and machines in our lives are built upon various control technologies. This fact is really amazing. However, more amazingly, the control technology originated as a governor that was made by James Watt in 1769 during the industrial revolution. The technology was born so as to regulate the rotational velocity of a centrifugal governor, and was initially a simple mechanism. The concept has been extended to a broad array of machines over time, and finally it has become a control theory. Now, we try to develop a simple mechanism to regulate the concentration of a target molecule. It would be just a small step in controlling biochemical reaction systems. We have named our proposal the “Molecular Governor,” indicating our strong desire for future expansion. We believe that it will change our lives as Marco would have achieved in our movie.
1.3 Theory
The following animation shows the state that the density of molecules is controlled through a membrane, and we will control the density of molecules x2 existing in there.Molecules x1existing outside a membrane react with signal molecules e1. Then, molecules x2 is generated.Molecules x2 can permeable a membrane freely and go in and out of that.Also, the density of molecules x2 is changed by that of signal molecules e1 from the outside.

Movie.1
As for the membrane, there are holes to permeate molecules, and molecules x2 are used for a reaction with molecules G, and generate molecules H.Thus, molecules x2 permeate a membrane in the ratio of uniformity and are used equally. Thereby we can make the density of molecules x2 whose are in the membrane a constant value.
1.3.1 Control of the molecule concentration

Fig.2 permeation of a membrane

Fig.1 reation scheme
To control the concentration of molecules implies that the concentration of a particular molecule corresponds to target value at the steady state and we can sets the target value freely. Therefore, we design the system to synchronize the density of molecules which we want to control with aim density at the steady state. This time we control the density of molecules with a membrane showing in following Fig1.
We explain a model showing in Fig1. Existing molecules x1 from outside a membrane changes to molecules x2 by action of signal molecules e1. The membrane shall be able to permeable x1 and x2 molecules(in Fig.2). We assume x2 after having permeated a membrane x4 and it the output molecules in this system. Similarly, we assume x1 after having permeated a membrane x3, and the x4 molecules change to x3 inside the membrane.
In other words, the concentration of x2 molecules rises while the concentration of x1 molecules decreases after a reaction with signal molecules e1 from the outside. As the concentration of x2 molecules rises, the x2 molecules permeate a membrane, and the concentration of output molecules x4 rises. The concentration of a molecule x4 is used for a reaction to generate x3 and moves to the outside of the membrane, and finally output molecules x4 agrees to target value.
1.3.2 Proof
We prove that output molecules x4 accords to aim density in this system.
These systems are given by the following equations(1).
Let xp be defined by
By differentiating Eq.(2) and we obtain (3),
When we assume that the value of x1 is much larger than that of K2, and the value of x4 is much smaller than that of K5, we have
Now, we consider a steady state of xp. Then, we obtain
By calculating the following equation,
We have
From (7)and(8), we obtain the following system, where α and β are positive constants.
Equation.(9) shows that x4 reaches to the target concentration x4* by the action of xp.
This shows that the density of output molecules x4 accords to target value by an effect of xp at the steady state. Additionally this implies that we able to change the targeted value by regulating density of a signal molecule e1 from the outside. Furthermore, even if other molecules existed, the targeted value is not affected if the molecules don’t reaction with molecules x1.
1.3.3 Simulation result
The parameters that we used for this simulation are in the table. 1, and theoretical values obtained from these parameters are in table.2.

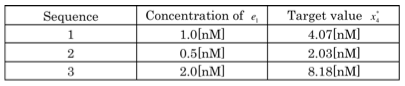
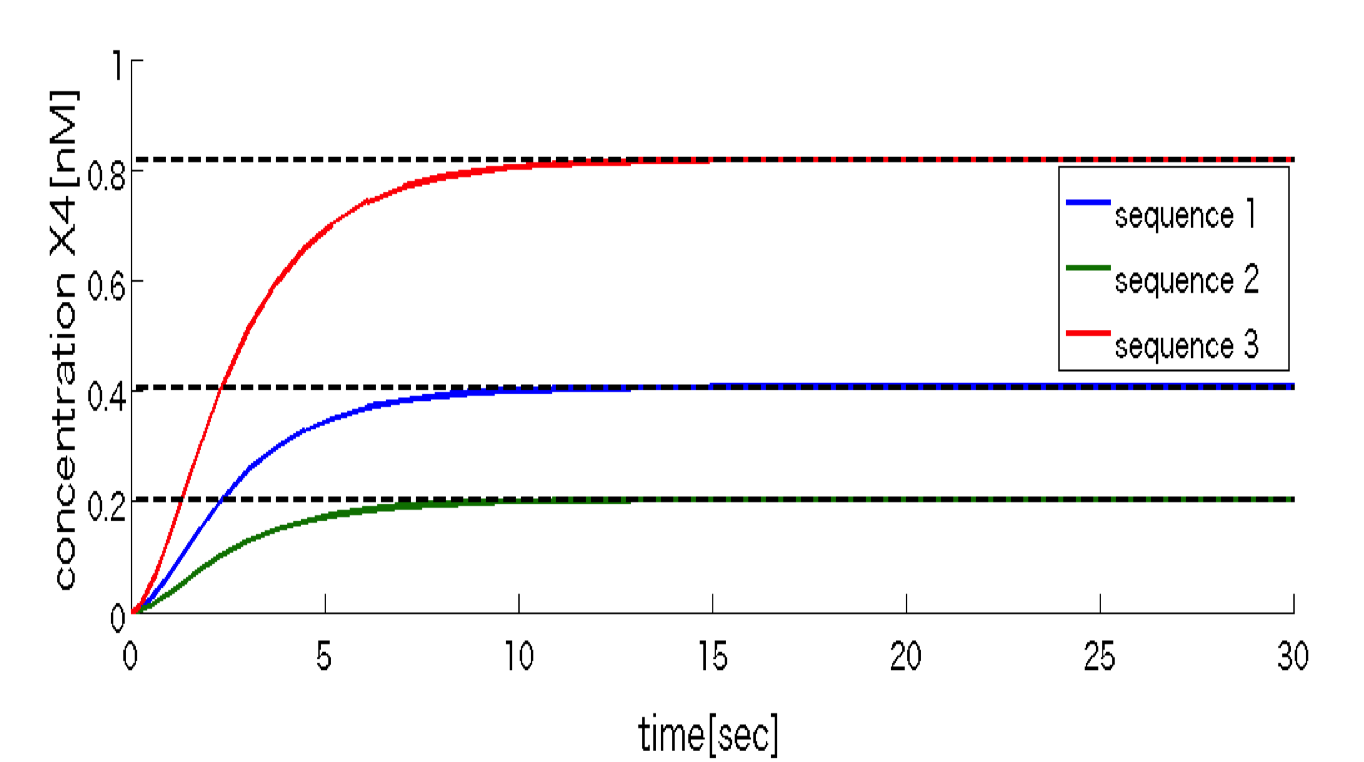
Fig.3 simulation result(The dashed line denote the target
concentration in each signal molecule e1.)The result of Fig.3 indicates that the concentration of molecule x4 reaches the target value x4* at the steady state, and that is variable by the density of signal molecules e1 from the outside.

